
[자료구조] 스택, 큐 (feat. java)
zl존석동
·2022. 1. 12. 20:20
스택과 큐에 대해 공부해보고
자바로 간단하게 구현해보자
Stack? Queue?
데이터를 저장할 수 있는 기본적인 구조로 선형 자료구조입니다.
선형 자료구조란?
하나의 자료 뒤에 하나의 자료가 있는 데이터가 순차적으로 나열되어 있는 것을 말한다.
Stack?

- 한 쪽 끝에서만 데이터를 넣거나 뺄 수 있는 LIFO(Last In First Out) 자료구조입니다.
- 데이터를 추가할 때는 밑에서부터 쌓아올리고 뺄 때는 위에 있는 것 부터 뺀다고 생각하면 될 것 같습니다.
어릴 때 먹던 콘 아이스크림을 생각해봅시다.
콘을 손에 들고 색색의 아이스크림들을 조금이라도 더 먹어 보겠다고
동그란 모양으로 퍼다가 미친듯이 쌓아올릴 것입니다.
이렇게 아이스크림을 쌓아 올리는 과정(데이터의 삽입)을 Push 라고 하며
쌓은 아이스크림을 먹는 과정(데이터의 삭제)를 Pop 이라고 합니다.
스택 활용
- 재귀 알고리즘
- 웹 사이트 검색 뒤로가기
- 아이스크림 통을 들고 퍼먹는 나의 모습
자바 배열로 구현하기
public class Main {
public static void main(String[] args) {
MyStack<Integer> myIntStack = new MyStack<>(5);
myIntStack.push(5);
myIntStack.peek();
myIntStack.pop();
}
}
class MyStack<T> {
T[] stack;
int top;
int size;
public MyStack(int size) {
this.size = size;
stack = (T[]) new Object[size];
top = -1;
}
public void push(T item) {
if (!isFull()) {
stack[++top] = item;
}
}
public T pop() {
if (!isEmpty()) {
return stack[top--];
}
return null;
}
public T peek() {
if (!isEmpty()) {
return stack[top];
}
return null;
}
private boolean isFull() {
return this.top == size - 1;
}
public boolean isEmpty() {
return top == -1;
}
}
배열 방식은 구현도 쉽고 처리속도가 빠르지만 최대 데이터 개수가 한정되어있습니다.
스택에 저장하여 처리해야할 데이터 개수가 명확할 때 사용하면 좋지 않을까 생각합니다.
LinkedList 로 구현하기
public class Main2 {
public static void main(String[] args) {
MyLLStack<Integer> myl = new MyLLStack<>();
myl.push(5);
myl.push(4);
myl.push(3);
myl.pop();
System.out.println(myl.peek());
}
}
class Node<T> {
T item;
Node next;
public Node(T item) {
this.item = item;
this.next = null;
}
void linkNext(Node node) {
this.next = node;
}
Node getNext() {
return next;
}
}
class MyLLStack<T> {
Node top;
public MyLLStack() {
this.top = null;
}
public void push(T data) {
// 입력받은 새로운 데이터에 대한 노드 생성
Node n = new Node(data);
//현재 top 위치에 있는 노드에 새로 생성된 노드를 다음 데이터로써 연결함
n.linkNext(top);
top = n;
}
public void pop() {
top = top.getNext();
}
public T peek() {
return (T) top.item;
}
}
배열보다 복잡하긴 하지만 스택의 크기가 고정되어있지 않다는 장점을 가집니다.
물론 자바에서 제공해주는 Stack 클래스나 Deque 인터페이스를 활용하면 훨씬 더 쉽게 사용할 수 있습니다.
Queue?
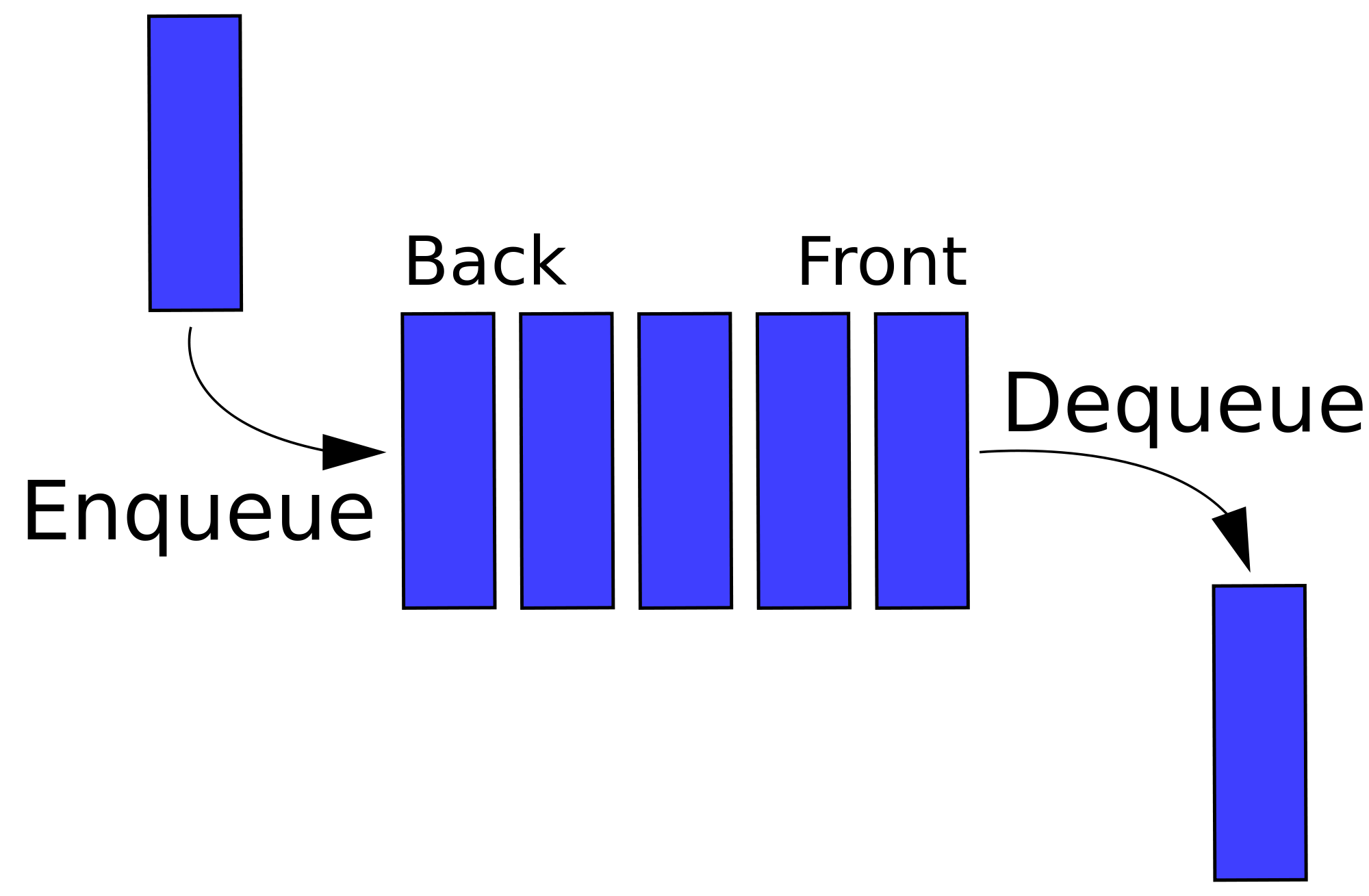
먼저 들어온 데이터가 먼저 나가는 FIFO(First In First Out) 의 자료구조입니다.
큐의 한쪽 끝인 Front 는 삭제연산만 수행하고
다른 한쪽 끝인 Rear 는 삽입연산만 수행하게 됩니다.
큐 활용
- 프로세스 관리
- 프린터 출력 대기
- 코로나 검사 받으려고 줄 서 있는 나
자바 배열로 구현하기
스택과 구현이 비슷하지만 스택에서 top 이라는 속성만으로 입력 삭제가 모두 가능했던 것과 달리
큐에서는 입력과 삭제가 수행되는 위치가 달라 front, rear 두가지 속성이 필요합니다.
public class QueueExam1 {
public static void main(String[] args) {
MyQueue<Integer> mq = new MyQueue<>(5);
mq.add(5);
mq.add(4);
mq.add(3);
System.out.println(mq.pop());
System.out.println(mq.peek());
}
}
class MyQueue<T> {
private int rear;
private int front;
private T[] queue;
private int size;
public MyQueue(int size) {
this.size = size;
queue = (T[]) new Object[size];
front = 0;
rear = 0;
}
public void add(T data) {
if (!isFull()) {
this.queue[rear++] = data;
}
}
public T pop() {
if (!isEmpty()) {
return queue[front++];
}
return null;
}
public T peek() {
if (!isEmpty()) {
return queue[front];
}
return null;
}
private boolean isFull() {
return rear == size - 1;
}
public boolean isEmpty() {
if (front == rear) {
front = 0;
rear = 0;
}
return front == rear;
}
}
역시나 배열로 구현하면 처리할 수 있는 데이터 수에 제한이 있습니다.
또한 (front == rear) : 배열이 비었을 때 다시 front 와 rear 를 다시 초기값으로 설정해줘야 지속적으로 사용할 수 있습니다.
LinkedList 로 구현하기
public class QueueExam2 {
public static void main(String[] args) {
MyLLQueue<Integer> ml = new MyLLQueue<>();
ml.add(5);
ml.add(4);
ml.add(3);
System.out.println(ml.pop());
System.out.println(ml.peek());
}
}
class MyLLQueue<T> {
// 삭제연산만 할 front
private Node front;
// 삽입연산만 할 rear
private Node rear;
public MyLLQueue() {
this.front = null;
this.rear = null;
}
public void add(T data) {
Node n = new Node(data);
if (isEmpty()) {
front = n;
rear = n;
return;
}
rear.linkNext(n);
rear = n;
}
public T peek() {
return (T) front.item;
}
public T pop() {
Node n = front;
front = front.getNext();
return (T) n.item;
}
public boolean isEmpty() {
return front == null && rear == null;
}
}
Queue 도 자바에서 제공해주는 Queue<E> 인터페이스를 통해 쉽게 활용할 수 있습니다.
양쪽 끝에서 삽입과 삭제가 모두 가능한 Stack 과 Queue 를 합쳐 놓은 개념인 Deque 도 있습니다.
상황에 맞게 어떤 자료구조를 어떤 방법으로 활용할지 잘 판단하는 것이 중요하지 않을까 싶습니다.
https://ko.wikipedia.org/wiki/%EC%8A%A4%ED%83%9D

