[Algorithm] 이분 탐색

 

이분탐색(Binary Search) 에 대해 공부해보자

---

 

 

 

 

탐색?

 

 

많은 데이터 속에서 원하는 데이터를 찾는 것

 

 

 

완전 탐색

 

 

가능한 모든 경우의 수를 탐색하는 것으로 반복문 또는 재귀함수 등을 사용해 구현하게 된다.

 

자원 소모가 크지만 반드시 원하는 데이터를 찾을 수 있다.

 

자원 소모가 크다고 하나 반드시 필요한 상황 또한 있다.

 

---

컴퓨터를 사고 싶은데 돈이 아까워서 친구 핸드폰으로 구매하는 상황이라고 해보자

 

핸드폰 결제 문자 메시지 인증이 4자리의 숫자라는 것을 아는 나는

 

친구에게 인증번호를 물어보지 않아도 1000 부터 9999까지 모두 대입해보다 보면 결국 인증번호를 맞출 수 있게 된다.

 

물론 시간제한도 있고 현실은 그 전에 한 3번 틀리면 내 세션에서의 인증이 아예 막혀버리겠지만

 

그런 시스템을 배제한다면 이론 상으로는 모두 대입해보면 인증번호를 찾을 수 있는 것이다.

 

 

---

공부 목적으로 클라우드 서버를 열어놓은 적이 있었는데

 

쉘 접속 로그를 확인했을 때 접속 시도를 이틀 동안 1분마다 하는 미친놈이 있었다.

 

아마 가능할 것 같은 비밀번호의 세트를 만들어 무작위로 모두 넣어보고 있었을 것이다.

 

그걸 보고 5번 이상 쉡 접속을 실패한 IP를 영구적으로 차단해버리는 설정을 하긴 했지만 무서웠다 ㅠㅠ

 

이런 상황 또한 완전탐색을 시도한 것이지 않을까 생각한다.

 

 

 

 

위 처럼 자원에 한정이 없고 구해야 하는 답이 명확하지 않고 범위 또한 명확하지 않을 때

 

원하는 값을 찾아야 할 경우 완전탐색이 유효하지 않을까 생각한다.

 

 

 

 

 

 

 

이분 탐색

 

 

정렬된 데이터에서 특정 값의 위치를 찾는 탐색방법이다.

 

데이터 리스트에서 중간 값을 Pivot 으로 설정해 찾아야 하는 값과 비교해 범위를 줄여나가는

 

Up and Down 게임이라고 볼 수 있다.

 

구하고자 하는 답의 범위가 명확하고 방향성이 있다면 활용할 수 있는 탐색 방법이다.

 

완전탐색과 비교하며 예시를 통해 이해해보도록 하였다.

 

 

 

 

예제

 

 

술자리에서 준건이는 다음과 같은 게임을 제시했다.

 

1 부터 10 까지의 숫자 중 내가 하나를 고를게
무슨 숫자를 선택했는지 맞춰봐!
한 번 못 맞출 때마다 너는 한 잔씩 마셔야 해!
대신 못 맞출 때마다 니가 찍은 수가 내가 고른 수보다 더 큰지 작은지 알려줄게 

 

준건이가 8을 골랐다고 생각하자.

 

 

 

완전탐색

 

 

술에 취해 정신이 없었던 동석이는 더 큰수 작은 수 같은건 생각하기 싫었고

 

다음과 같이 10개의 숫자를 무작위로 순서대로 불러보기로 했다.

 

 

8이 정답이기에 동석이는 재수없게도 10번만에 정답을 찾게 되어 9잔의 술을 마셔야 했다.

 

이런 경우를 완전 탐색 했다고 할 수 있다.

 

재수가 없었던 동석이는 10번만에 정답을 찾게 되었기 때문에 최악의 경우 O(n) 의 시간 복잡도를 가지게 된다.

 

 

 

 

이분탐색

 

 

머리가 좋았던 경빈이는 10개의 숫자를 순차적으로 나열하여 먼저 하나를 고르고

 

준건이가 제시해준 숫자의 크기와 비교하여 찾아나갈 계획을 가지게 되었다.

 

경빈이는 중간에 위치한 6을 먼저 선택하고 준건이에게 제시했다.

 

 

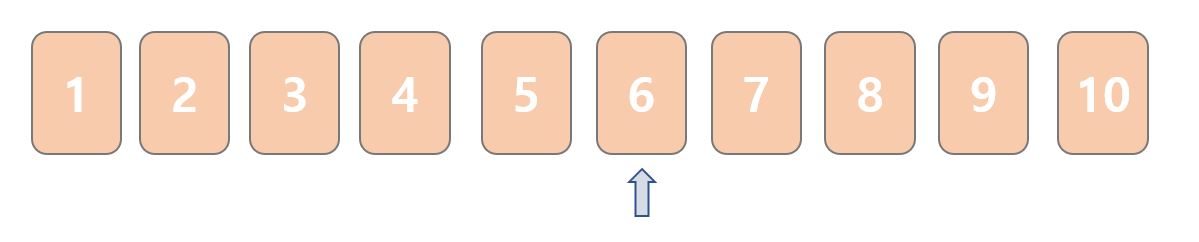
준건 : Up!

 

 

6보다 크다고 들은 경빈이는 7,8,9,10 중 하나라는 사실을 깨닫고 6 이하의 수는 모두 배제하기로 하였다.

 

7, 8, 9 ,10 의 중간 위치의 숫자인 9를 고르고 다시 제시했다.

 

 

준건 : Down!

 

 

이제 용의선상에 있는 숫자는 7과 8 뿐이었다.

 

둘의 중간 위치인 8을 선택하게 되는 경빈이는 드디어 정답을 맞출 수 있었다.

 

 

멍청한 동석이가 10번만에 찾아낸 값을 경빈이는 단 3번만에 찾을 수 있었다.

 

만약 최악의 경우로 준건이가 1을 선택했었다 하더라도

 

경빈이는 6 -> 3 -> 2 -> 1 순서대로 4번만에 값을 찾아낼 수 있었을 것이다.

 

 

만약 32개의 숫자 중 하나를 고르는 것이었다 하더라도

 

1을 찾는데는 16 -> 8 -> 4 -> 2 -> 1로 5번만에 찾을 수 있었을 것이다.

 

동석이가 재수 없었다면 32번만에 값을 찾을 수 있다는 것에 비해 

 

경빈이는 아무리 재수가 없어도 5번만에 값을 찾을 수 있는 것이다.

 

위처럼 이분 탐색이 가능한 상황(정렬 가능한 명확한 범위에 비교가 가능한 값들로 구성된)이라면

 

O(n) 의 시간 복잡도를 O(log2(n)) 으로 줄일 수 있다.

 

 

 

 

코드로 구현하기

 

 

    /** 
    * 이분 탐색
    * @param arr 정렬된 배열 
    * @param value 찾아야 하는 값
    * @return 해당 값의 인덱스 / 없으면 -1
    */
    int search(int[] arr, int value) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (value < arr[mid]) {
                right = mid - 1;
                continue;
            }
            if (value > arr[mid]) {
                left = mid + 1;
                continue;
            }
            if (value == arr[mid]) {
                return mid;
            }
        }
        return -1;
    }

 

 

1920번: 수 찾기

 

딱 이분탐색이라는 알고리즘만 활용해 볼 수 있는 쉬운 문제인 것 같다.

 

위의 예시 메소드와 다르게 문제에서는 값의 존재여부에 관심을 두고 있다.